Nicole Oresme
Nicole Oresme or Nicolas d'Oresme (c.1323 - July 11, 1382) was one of the most original thinkers of the fourteenth century, developing concepts and ideas which anticipated the scientific breakthroughs of scientists centuries later. An economist, mathematician, physicist, astronomer, philosopher, psychologist, and musicologist, he was also a passionate theologian and Bishop of Lisieux. He served as counselor of King Charles V of France, and at his behest translated several works of Aristotle into French and wrote numerous works popularizing science and learning.
Oresme evolved a geometrical method of plotting speed or intensity over time or distance, and offered the first proof of Merton’s theory. He also developed a language of ratios, introduced by Thomas Bradwardine, to relate speed to force and resistance, and applied it to physical and cosmological questions. He made a careful study of musicology and used his findings to develop the use of irrational exponents and the first theory that sound and light are a transfer of energy that does not displace matter. He suggested that color is a quality of light, and advanced a theory of the atmospheric refraction of light.
Oresme was especially interested in the psychology of perception and suggested that most qualities and attributes, rather than being perceived objectively, existed only in the human consciousness and were elaborately constructed from conscious and unconscious assumptions and sensory experiences. He developed a theory of probability which he used to evaluate the likelihood of a perception being accurate.
Life
Nicole Oresme was born c.1320-1325 in the village of Allemagne (today's Fleury-sur-Orne) in the vicinity of Caen, Normandy, in the Diocese of Bayeux. Nothing is known about his family except that he was of Norman descent. Oresme attended the royally sponsored and subsidized College of Navarre, an institution for students too poor to pay their expenses while studying at the University of Paris, indicating that he probably came from a peasant family.
Oresme studied the “artes” in Paris before 1342, together with Jean Buridan (often called founder of the French school of natural philosophy), Albert of Saxony and perhaps Marsilius of Inghen, and there received the Magister Artium. A recently discovered papal letter of provision granting Oresme an expectation of a benefice establishes that he was already a regent master in arts by 1342. This early dating of Oresme's arts degree places him at Paris during the crisis over William of Ockham's natural philosophy.
In 1348, he was a student of theology in Paris; in 1356, he received his doctorate and in the same year he became grand master (grand-maître) of the College of Navarre. Many of his most thoughtful Latin treatises antedate 1360, and show that Oresme was already an established schoolman of the highest reputation. He attracted the attention of the royal family, and was brought into intimate contact with the future Charles V in 1356. Charles began to act as regent in 1356, while his father John II was in captivity in England, and from 1364 until 1380, was King of France. On November 2, 1359, Oresme became "secretaire du roi" and upon Charles’ coronation on April 8, 1364, he became chaplain and counselor to the king. Charles appears to have had the highest esteem for Oresme’s character and talents, often followed his counsel, and made him write many works in French for the purpose of popularizing the sciences and of developing a taste for learning in the kingdom. At Charles’s insistence Oresme delivered a discourse before the papal court at Avignon, denouncing the ecclesiastical disorder of the time. As an intimate friend and advisor to King Charles, "Le Sage," until his death in 1380, Oresme was in a position to influence Charles’ progressive political, economical, ethical and philosophical thinking. Oresme was the most important of a circle of intellectuals, including Raoul de Presle and Philippe de Mézières, at Charles’ court.
Oresme, as the grand master of Navarre, was sent by the dauphin to seek a loan from the municipal authorities of Rouen in 1356 and then in 1360. While still grand master of Navarre, he was appointed archdeacon of Bayeux with the support of Charles in 1361. It is known that Oresme unwillingly surrendered the interesting post of grand master. Charles may have influenced his father, King John II, to grant Oresme a series of increasingly important appointments. On November 23, 1362, the year he became master of theology, Oresme was appointed canon of the Cathedral of Rouen. At the time of this appointment, he was still teaching regularly at the University of Paris. On February 10, 1363, he was made a canon at La Saint Chapelle, given a semiprebend and on March 18, 1364, and was elevated to the post of dean of the Cathedral of Rouen. During his tenure in these successive posts at the Cathedral of Rouen (1364-1377), documents related to affairs of the University show that Oresme spent considerable time in Paris, but it not known if he also continued to teach there.
Letters sent by Charles to Rouen from August 28 to November 11, 1372, indicate that Oresme began working on translations at the request of the king, and took up residence in Paris. Oresme began his translation of Aristotle’s Ethics in 1369, and completed it in 1370; Aristotle’s Politics and Economics may have been completed between the years of 1372 and 1374; and the De caelo et mundo in 1377. Oresme received a pension from the royal treasury as early as 1371 as a reward for his labors. Oresme’s work for Charles and the royal family earned him an appointment, on August 3, 1377, to the post of Bishop of Lisieux. It appears that Oresme did not take up residency at Lisieux until September of 1380, the year of Charles’ death. Little is known of the final years of his life. Oresme died in Lisieux on July 11, 1382, and was buried in the cathedral church.
Thought and Works
Nicole Oresme made significant contributions to late medieval natural philosophy. He studied and wrote about philosophy, mathematics, economics, physics, musicology, and psychology, and anticipated the ideas of early modern scientists such as Copernicus, Galileo and Descartes. He developed a geometric model to quantify and compare the intensities of qualities and of speeds. Oresme also developed the language of ratios, introduced by Thomas Bradwardine to relate speed to force and resistance, and applied it to physical and cosmological questions. He made a careful study of musicology and used his findings to develop the use of irrational exponents and the first theory that sound and light are a transfer of energy that does not displace matter. More than thirty-four books and treatises by Nicole Oresme are extant.
His translations of Aristotle’s works introduced a number of technical terms into the French language. He did not agree with Aristotle that “qualities” existed objectively, and worked extensively to prove that they were subject to the perception of the human mind. He studied the influence of the subconscious mind on perception, and also the physical phenomena, such as atmospheric distortion, which cause errors in perception. He also developed the use of probability ratios to determine the extent to which accurate perception was possible. (For a complete list, visit Nicole Oresme Bibliography by Ulrich Taschow)
Economics
Oresme's views on economics are contained in Commentary on the Ethics of Aristotle, of which the French version is dated 1370; Commentary on the Politics and the Economics of Aristotle, French edition, 1371; and Treatise on Coins (De origine, natura, jure et mutationibus monetarum). These three works, written in both Latin and French, mark Oresme as a precursor of the science of political economy, and reveal his mastery of the French language. Oresme created a number of French scientific terms and anticipated the usage of Latin words in the scientific language of the eighteenth century.
The French Commentary on the Ethics of Aristotle was printed in Paris in 1488; that on the Politics and the Economics, in 1489. The Treatise on coins, De origine, natura, jure et mutationibus monetarum was printed in Paris early in the sixteenth century, also at Lyons in 1675, as an appendix to the De re monetaria of Marquardus Freherus, is included in the Sacra bibliotheca sanctorum Patrum of Margaronus de la Bigne IX, (Paris, 1859), 159, and in the Acta publica monetaria of David Thomas de Hagelstein (Augsburg, 1642). The Traictié de la première invention des monnoies in French was printed at Bruges in 1477.
Mathematics
His most important contributions to mathematics are contained in Tractatus de configuratione qualitatum et motuum, still in manuscript. An abridgment of this work printed as the Tractatus de latitudinibus formarum of Johannes de Sancto Martino (1482, 1486, 1505 and 1515), has for a long time has been the only source for the study of Oresme's mathematical ideas. In a quality, or accidental form, such as heat, the Scholastics distinguished the intensio (the degree of heat at each point) and the extensio (as the length of the heated rod). These two terms were often replaced by latitudo and longitudo, and from the time of Thomas Aquinas until far into the fourteenth century, there was lively debate on the latitudo formae. For the sake of clarity, Oresme conceived the idea of employing what, in modern terminology, we call rectangular co-ordinates. A length proportionate to the longitudo, representing space and time, was used as a base line, and from that line perpendicular lines, the latitudo, were erected representing the intensity or position of the variable at the corresponding time or length on the base line. The ends of these vertical lines were then connected by a curving line which illustrated the variations in intensity. The “latitudo” might vary or remain constant; a constant or uniform intensity would be represented by a horizontal line parallel to the base line, which Oresme designated the “latitudo uniformis;” any variation was called “latitude difformis..”
Though he did not use numerical equivalents for the points on his graph, Oresme’s concept was an important one in the later development of analytical geometry.
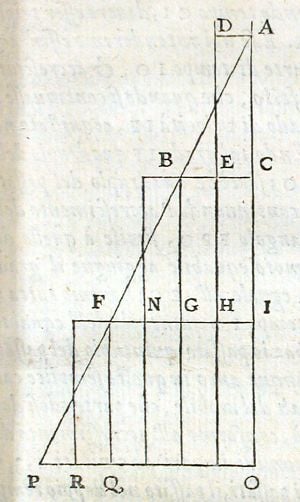
Oresme designated the area of the resulting geometrical figure the “mensura” or “quantitas,” and demonstrated that if the speed of an accelerating body (“uniformiter difformis”) were plotted over a certain period of time, the area (“quantitas”) of the resulting geometric figure was equal to the “quantitas” of a second geometric figure formed by plotting a constant speed (“latitudo uniformis”) equal to the mean between the lowest and highest speeds of the first figure over the same period of time. This was the first proof of Merton's theorem, that the distance traveled in a fixed time by a body moving under uniform acceleration is the same as if the body moved at a uniform speed equal to its speed at the midpoint of the time period. It was taught at Oxford by William Heytesbury and his followers, then at Paris and in Italy by subsequent followers of this school. In the middle of the sixteenth century, the Dominican Domingo de Soto applied the law to the uniformly accelerated falling of heavy bodies and to the uniformly decreasing ascension of projectiles. Oresme's demonstration resembles the laws later developed by Galileo, but there is no evidence that Galileo was directly influenced by Oresme’s work.
In Algorismus proportionum and De proportionibus proportionum, Oresme developed the first use of powers with fractional exponents, calculation with irrational proportions (proportio proportionum). The basis of this method was Oresme’s equalization of continuous magnitudes and discrete numbers, an idea that Oresme took out of musical monochord-theory (sectio canonis). In this way, Oresme overcame the Pythagorean prohibition of regular division of Pythagorean intervals like 8/9, 1/2, 3/4, 2/3 and provided a tool to generate "equal tempo," anticipating Simon Stevin. Here an example for the equal division of an octave in 12 parts:
Oresme’s interest in limits, threshold values and infinite series by means of geometric additions (Tractatus de configurationibus qualitatum et motuum, Questiones super geometriam Euclidis) prepared the way for the infinitesimal calculus of Descartes and Galileo. He proved the divergence of the harmonic series, using the standard method still taught in calculus classes today.
Musicology
Many of Oresme’s insights in mathematics, physics, philosophy, and psychology, which anticipate modern science, were closely bound up with musical models. The Musica functioned as a sort of "computer of the Middle Ages" and provided a means of testing theories in mathematics, physics, perception and psychology.
Oresme's overarching aesthetic approach to natural phenomena was based on the conviction that the aesthetic evaluation of (graphically representable) sense experience provided an adequate principle of analysis. Music played an important role as the model for the "aesthetics of complexity and of the infinite" favored by the intellectual thought of the fourteenth century. Oresme experimented with the parameters of sound (the sonus) both on the microstructural, acoustical level of the single tone and on the macrostructural level of unison or polyphonic music. In attempting to capture analytically the various physical, psychological and aesthetic parameters of sound according to extensio (time intervals) and intensio (pitch), Oresme wished to establish criteria for infinitely variable grades of pulchritudo (beauty, harmony) and turpitudo (ugliness, dissonance). He developed the most complete mathematical description of musical phenomena before Galileo's Discorsi.
Oresme's configuratio qualitatum, and the functional pluridimensionality associated with it, are closely related to contemporary musicological diagrams, and to musical notation, which both quantifies and visually represents the variations of sound.
Music helped to provide examples of the various types of uniform and difform configurations Oresme had developed, and to support the idea that certain configurations endowed qualities with specific effects, aesthetic or otherwise, which could be analytically captured by their geometric representation.
Oresme used irrational exponents to discover “partial tones” or "overtones" three centuries before Marin Mersenne. He also recognized the relation between overtones and tone color, which he explained in a detailed and complex mathematical theory.
Oresme’s Tractatus de configuratione et qualitatum motuum presented a mechanistic understanding of sound sonus as a specific discontinuous type of movement (vibration), of resonance as an overtone phenomenon, and of the relation between consonance and dissonance, which went beyond the successful but incorrect coincidence theory of consonance later formulated in the seventeenth century. A demonstration such as Oresme's, of a correspondence between a mathematical method (configuratio qualitatum et motuum) and a physical phenomenon (sound), was rare in the fourteenth century, and the sections of the Tractatus de configurationibus dealing with music are milestones in the development of the methods of quantifying that characterizes modern science.
Oresme, whose friend Philippe de Vitry was a famous music-theorist, composer and Bishop of Meaux, dealt nearly with every area of modern musicology:
- acoustics (in Expositio super de anima, Quaestiones de anima, De causis mirabilium, De configurationibus, De commensurabilitate vel incommensurabilitate),
- musical aesthetics (in De configurationibus,, De commensurabilitate vel incommensurabilitate),
- physiology of voice and hearing (in Quaestiones de sensu, Expositio super de anima),
- psychology of hearing (in Quaestiones de anima, De causis mirabilium, Quaestiones de sensu),
- musical theory of measurement (in Tractatus specialis de monocordi,[1] De configurationibus, Algorismus proportionum),
- music theory (in De configurationibus),
- musical performing (in De configurationibus),
- music philosophy (in De commensurabilitate vel incommensurabilitate).
Oresme formulated the first correct theory of wave-mechanics, “theory of species“ (multiplicatio specierum), positing that sound and light involve the transport of pure energy without the deformation of any matter. Oresme uses the term species in the same sense as the modern term “wave form.")
Psychology
Oresme used empirical methods to investigate the phenomena of the human psyche. Like others of the "Parisian Psychological School" (Jean Buridan, Barthelemy de Bruges, Jean de Jandun, Henry of Hesse (Heinrich von Langenstein)), Oresme accepted the activity of "inner senses" (sensus interior) and recognized the subjectivity, complexity and constructive tendencies of human perception of the world. Oresme’s thought on the subject was typical of fourteenth century scholarship, and his work was closely related to that of the scientists of optics (Alhazen, Roger Bacon, Witelo, John Pecham). Oresme, however, proposed innovative ideas in the fields of cognitive psychology, psychology of perception, psychology of consciousness and psycho-physics.
Oresme examined the role of the psychological "unconscious" in perception and behavior. His "theory of unconscious conclusions of perception" and his “hypothesis of two attentions,” involving a conscious and an unconscious attention, anticipate the psychology of the twentieth century. Oresme’s “theory of cognition” asserted that no thought-related concepts, such as categories, terms, qualities and quantities, exist outside of human consciousness. He argued that so-called "primary qualities" such as size, position, shape, motion, and rest were not 'objective' in outer nature, but should be seen as very complex cognitive constructions of the psyche under the individual conditions of the human body and soul. Because reality is only in the instant ("expansionless moment,” “instantia”), Oresme reasoned that no motion could exist except in consciousness. This meant that motion was a result of human perception and memory, an active composition of "before" and "later." In the case of sound, Oresme wrote: "If a creature would exist without memory, it never could hear a sound…"
Oresme solved the "dualism" of the physical and the psychical world by using the three-part schema “species - materia - qualitas sensibilis” (“information” – “medium” – “meaning”) of his "species-theory." The transportable species (information), like a waveform of sound, changes its medium (wood, air, water, nervous system, etc.) and the inner sense (sensus interior) constructs, by means of "unconscious conclusions," a subjective meaning from it.
In his studies of aesthetics in music, Oresme formulated a modern subjective "theory of perception," which explained that aesthetic perception is not perception of objective beauty in God’s creation, but a constructive process of perception, which results in the perception of beauty or ugliness by the senses of the perceiver. Therefore, every individual perceives a different "world," based on a complex combination of conscious and unconscious circumstances.
Oresme’s ideas of psyche were strongly mechanistic. Physical and psychical processes were equivalent in their structure and motion (configuratio qualitatum et motuum). Every structure had a qualitative (psychical) and a quantitative (physical) moment; therefore psychological processes (intensities) could be measured like physical ones. Thus, Oresme supplied the first scientific proposal for measurement of psyche and (against the views of Aristotle and the Scholastics) even of the immaterial soul.
Oresme focused his attention most strongly on the psychology of perception. He composed a treatise, unique for the Middle Ages, on perception and its disorder and delusion (De causis mirabilium), examining each of the physical senses (sight, hearing, touch, smell, taste) and the cognitive functions. By analyzing delusions and disorders, Oresme recognized many essential laws of perception, such as the shape law ("Gestaltgesetze") and the limits of perception (maxima et minima).
Natural philosophy
Oresme’s philosophical thinking reflects the complexity of his scientific and mathematical works. He opposed the Aristotelian-scholastic dogma of the unchanging substantial species and endless repetitions; just as the model of the machina musica showed that in music, with a limited number of proportions and parameters, someone could produce very complex, infinitely varying and never-repeating structures (De configurationibus qualitatum et motuum, De commensurabilitate vel incommensurabilitate, Quaestio contra divinatores), so the universe could form ever-changing structures from a set of parameters, principles and elements of matter. In Oresme’s linear-progressive world, at any given time everything was unique and new, and in the same way human knowledge of the universe was ever-changing. Oresme created a dynamic structural model for the constitution of the substantial species and individuals found in nature, the so-called "theory of perfectio specierum." (De configurationibus qualitatum et motuu, Quaestiones super de generatione et corruptione, Tractatus de perfectionibus specierum). An Oresmian individual is a self-organizing system which arrives at its optimal state by defending itself from disturbing environmental influences.
Theories of probability
Oresme made an extensive investigation of statistical approximate values and measurements and margins of error, and a "theory of probabilities" which he applied to psychology as well as to physics and mathematics.
In De causis mirabilium, Oresme laid down two interdependent psychological rules regarding the probability of errors in perception due to unconscious judgements, in order to illustrate that perception is never an objective “photography” but a complex psychological construction without absolute evidence. In mathematics, Oresme anticipated modern stochastic by developing a tool to judge the quantitative likelihood that a certain event would occur (De proportionibus proportionum). Oresme used terms for his calculations of probability like verisimile, probabile / probabilius, improbabile / improbabilius, verisimile / verisimilius, / maxime verisimile and possibile equaliter, which had not been previously used in the context of probability, and were not used again until the seventeenth century.[2]
Appearance of ratios in nature
In his works De commensurabilitate vel incommensurabilitate, De proportionibus proportionum, Ad pauca respicientes, Oresme said, "If we take two unknown natural magnitudes like motion, time, distance, etc., then it is more probable (verisimillius et probabilius) that the ratio of these two is irrational rather than rational.” According to Oresme this theorem applied generally to all of nature, the earthly and the celestial world. It had great effect on Oresme’s views of necessity and contingency, and consequently on his view of the law of nature (leges naturae) and his criticism of astrology. It is evident that the inspiration for this probability theory came from Oresme’s work in music. The division of monochord (sectio canonis) clearly proved both to the sense of hearing and to mathematical reason that most of the divisions of chord produce irrational, dissonant intervals.
He examined the question as to whether the ratio of the periods of two heavenly bodies was a rational number asking: "…if anyone should make a mechanical clock, would he not make all the wheels move as harmoniously as possible?" He then answered his own question, arguing that the irrationality of ratios will not rob the heavens of their beauty and will also not be inconsistent with regular movement. Oresme also worked on infinite series and argued for an infinite void beyond the Earth.
Physics
Oresme’s physical teachings are set forth in two French works, the Traité de la sphère, twice printed in Paris (first edition without date; second, 1508), and the Traité du ciel et du monde, written in 1377 at the request of King Charles V, but never printed. In most of the essential problems of statics and dynamics, Oresme follows the opinions advocated in Paris by his predecessor, Jean Buridan de Béthune, and his contemporary, Albert of Saxony. In opposition to the Aristotelian theory of weight, which said that the natural location of heavy bodies is in the center of the world, and that of light bodies in the concavity of the moon's orb, Oresme countered by proposing the following: "The elements tend to dispose themselves in such a manner that, from the centre to the periphery their specific weight diminishes by degrees." Oresme thought that a similar rule may exist in worlds other than ours.
In Traité du ciel et du monde Oresme gave several strong arguments for the daily rotation of the earth, and solved the objections based on the texts of Holy Scripture with an interpretation which is used by Catholic exegetics of the present day. He finally concluded, though, that the evidence for the rotation of the earth was no stronger than the evidence that the earth was static.
Oresme was one of the first to deduce that color and light are of the same nature, applying observations taken from his study of musical “overtones” and “tone colors” to the mixture of colors on a spinning top. In his treatise De visione stellarum Oresme questioned whether the stars are really where they seem to be, and applied principles of optics to describe the curvature of light through atmospheric refraction.
Notes
Legacy
- Quotation: "Therefore, I indeed know nothing except that I know that I know nothing." Quodlibeta, MS Paris, BN lat. 15126, 98v
- A crater on the moon is named for Oresme.
ReferencesISBN links support NWE through referral fees
Primary sources
- Oresme, Nicole. An Abstract of Nicolas OreÌme's Treatise on the breadths of forms (The great books of St. John's) The St. John's bookstore, 1941.
- --------. De Proportionibus Proportionum and Ad Pauca Respicientes,
Wisconsin University Press, 1966.
- --------. The De moneta of Nicholas Oresme, and English Mint documents;: Translated from the Latin with introd. and notes (Medieval texts). Nelson, 1956.
- --------; Grant, Edward (Editor). Nicole Oresme and the Kinematics of Circular Motion, (University of Wisconsin Publications in Medieval Science) University of Wisconsin Press, 1971.
Secondary Sources
- Babbitt, Susan M. Oresme's Livre De Politiques and the France of Charles V, (Transactions of the American Philosophical Society). American Philosophical Society, 1985.
- Burton, Dan. Nicole Oresme's De Visione Stellarum (On Seeing the Stars): A Critical Edition of Oresme's Treatise on Optics And Atmospheric Refraction, With an Introduction, (Medieval and Early Modern Science). Scheduled for publication October, 2006.
- Copleston, Frederick, S. J.. A History of Philosophy, Volume III: Late Medieval and Renaissance Philosophy, New York: Image Books, Doubleday, 1993. pp. 160-168.
- Hansen, Bert. Nicole Oresme and the Marvels of Nature: A Study of His De Causis Mirabilium With Critical Edition, Translation, and Commentary, Studies and Texts, Pontifical Inst. of Mediaeval Studies, 1985.
- Menut, Albert D. Nicole Oresme: Highlights from His French Commentary on Aristotle's Politics, Coronado Press, 1979.
- Taschow, Ulrich. Nicole Oresme und der Frühling der Moderne: Die Ursprünge unserer modernen quantitativ-metrischen Weltaneignungsstrategien und neuzeitlichen Bewusstseins- und Wissenschaftskultur, Halle: Avox Medien-Verlag, 2003, 4 Books in 2 Volumes. ISBN 3936979006
External links
All links retrieved November 14, 2022.
- Oresme Biography from which some of the above article was taken, with friendly authorization of its author Ulrich Taschow. There you can also find the complete bibliography of Oresme's work and many other materials on Nicole Oresme
- Medieval Theories of Causation, Stanford Encyclopedia of Philosophy
General philosophy sources
- Stanford Encyclopedia of Philosophy
- The Internet Encyclopedia of Philosophy
- Paideia Project Online
- Project Gutenberg
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.

