Meson
| Meson | |
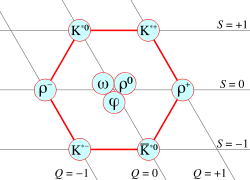
 Mesons of spin 0 form a nonet (Nine different possible pairs made from a certain set of quarks and antiquarks.) | |
| Composition: | Composite - Quarks and antiquarks |
|---|---|
| Family: | Hadron |
| Interaction: | Strong |
| Theorized: | Hideki Yukawa (1935) |
| Discovered: | 1947 |
| No. of types: | ~140 (List) |
| Spin: | Integer |
In the Standard Model of particle physics, a meson is a composite subatomic particle comprising one quark and one antiquark. Mesons are part of the hadron particle family—particles made of quarks. The other members of the hadron family are the baryons—subatomic particles comprising three quarks. The main difference between mesons and baryons is that mesons are bosons having an integer spin, while baryons are fermions having half-integer spin.[1][2] All mesons are unstable. Searches for exotic mesons that have different constituents are ongoing.[3]
Since mesons are composed of quarks, they participate in both the weak and strong interactions. Mesons with net electric charge also participate in the electromagnetic interaction. They are classified according to their quark content, total angular momentum, parity, and various other properties such as C-parity and G-parity. While no meson is stable, those of lower mass are nonetheless more stable than the most massive mesons, and are easier to observe and study in particle accelerators or in cosmic ray experiments. They are also typically less massive than baryons, meaning that they are more easily produced in experiments, and will exhibit higher energy phenomena sooner than baryons would. The mesons that scientists have most often detected are pions (pi mesons) and kaons (K mesons).
The residual strong force, which is responsible for holding protons and neutrons together in atomic nuclei, is currently explained mainly in terms of the exchange of mesons such as pions.
Prediction and discovery
Japanese theoretical physicist Hideki Yukawa was the first to predict the existence of mesons, in 1935. He suggested that they are carriers of the force that binds protons and neutrons together in atomic nuclei. For his prediction, Yukawa was awarded the Nobel Prize in Physics in 1949.
Yukawa called the particle meson, from the Greek word mesos, meaning "intermediate," because its mass was between that of an electron and a proton. He had originally named it mesotron, but was corrected by Werner Heisenberg (whose father was a professor in Greek at the University of Munich), who pointed out that there is no "tr" in the Greek word mesos.
The muon, when first discovered, was thought of as a meson, based on its similar mass and was named "mu meson." However, it did not show a strong attraction to nuclear matter and was found to be a lepton. The pion was the first true meson to be discovered. Cecil Powell made the discovery in 1947. Current theoretical models of intranuclear forces are quite complicated, but they are based on the notion that nucleon-nucleon interactions are mediated by meson exchange.
Some examples
A pion (pi meson) is constituted of an up or down quark and an antiquark. For instance, a pi-plus meson consists of an up quark and an anti-down quark.[3]
A kaon (K meson) consists of one up or down quark or antiquark and one strange quark or antiquark. For instance, a K-plus meson is made of an up quark and an anti-strange quark.[3]
Pseudoscalar mesons (spin 0), where the quark and antiquark have opposite spin, have the lowest rest energy. Next lowest in rest energy are vector mesons (spin 1), where the quark and antiquark have parallel spin. Both come in higher-energy versions, where the spin is augmented by orbital angular momentum.
Naming of mesons
The name of a meson is devised so as to indicate its main properties. Conversely, given a meson's properties, its name is clearly determined. The naming conventions fall in two categories based on "flavor:" Flavorless mesons and flavored mesons.
Flavorless mesons
Flavorless mesons are those mesons for which flavor quantum numbers are all equal to zero. This means that these quarks are quarkonium states (quark-antiquark pairs of the same flavor) or a linear superposition of such states.
The name of a flavorless meson is determined by its total spin S and total orbital angular momentum L. As a meson is composed of two quarks with s = 1/2, the total spin can only be S = 1 (parallel spins) or S = 0 (anti-parallel spins). The orbital quantum number L is thought of as produced by the revolution of one quark around the other. Usually, higher orbital angular momenta translate into a higher mass. These two quantum numbers determine the parity P and the charge-conjugation parity C of the meson:
- P = (−1)L+1
- C = (−1)L+S
When L and S are added together, the result is a total angular momentum quantum number J, with values ranging from |L−S| to L+S in single-unit increments. The different possibilities are summarized with the use of the term symbol 2S+1LJ (a letter code is used instead of the actual value of L) and the symbol JPC (here only the sign is used for P and C).
The different possibilities and the corresponding meson symbols are given in the following table:
| JPC = | (0, 2…)− + | (1, 3…)+ − | (1,2…)− − | (0, 1…)+ + | |
|---|---|---|---|---|---|
| Quark composition | 2S+1LJ = * | 1(S, D…)J | 1(P, F…)J | 3(S, D…)J | 3(P, F…)J |
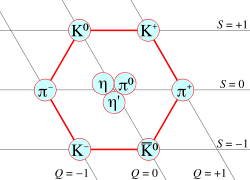
| † | I = 1 | π | b | ρ | a |
| ‡ | I = 0 | η, η’ | h, h’ | , ω | f, f’ |
| I = 0 | ηc | hc | ψ • | χc | |
| I = 0 | ηb | hb | Υ ** | χb |
Notes:
- * Note that some combinations are forbidden: 0− −, 0+ −, 1− +, 2+ −, 3− +...
- † First row form isospin triplets: π−, π0, π+ etc.
- ‡ Second row contains pairs of elements: φ is supposed to be a state, and ω a state. In the other cases, the exact composition is not known, so a prime is used to distinguish the two forms.
- • For historical reasons, 13S1 form of ψ is called J/ψ
- ** The bottomonium state symbol is a capital upsilon (may be rendered as a capital Y depending of the font/browser)
The normal spin-parity series is formed by those mesons where P=(−1)J. In the normal series, S = 1 so PC = +1 (i.e., P = C). This corresponds to some of the triplet states (triplet states appear in the last two columns).
Since some of these symbols can refer to more than one particle, some extra rules are added:
- In this scheme, particles with JP = 0− are known as pseudoscalars, and mesons with JP = 1− are called vectors. For particles other than those, the number J is added as a subindex: a0, a1, χc1, and so on.
- For most of ψ, Υ and χ states it is common to include spectroscopic information: Υ(1S), Υ(2S). The first number is the principal quantum number, and the letter is the spectroscopic notation for L. Multiplicity is omitted since it is implied by the symbol, and J appears as a subindex when needed: χb2(1P). If spectroscopic information is not available, mass is used instead: Υ(9460).
- The naming scheme does not differentiate between "pure" quark states and gluonium states, so gluonium states follow the same naming scheme.
- However, exotic mesons with "forbidden" quantum numbers JPC = 0− −, 0+ −, 1− +, 2+ −, 3− +… would use the same convention as the meson with identical JP numbers, but adding a J subindex. A meson with isospin 0 and JPC = 1− + would be denoted ω1.
When the quantum numbers of a particle are unknown, it is designated with an X followed by its mass in parentheses.
Flavored mesons
For flavored mesons, the naming scheme is a little simpler.
1. The meson name is given by the heavier of the two quarks. The order of quarks from heaviest to lightest is: t > b > c > s > d > u. However, u and d do not carry any flavor, so they do not influence the naming scheme. Quark t never forms hadrons, but a symbol for t-containing mesons is reserved anyway.
| quark | symbol | quark | symbol |
|---|---|---|---|
| c | D | t | T |
| s | b |
- For s and b quarks we get an antiparticle symbol. This is because the adopted convention is that flavor charge and electric charge must agree in sign. This is also true for the third component of isospin: Quark up has positive I3 and charge, quark down has negative charge and I3. The effect of that is: any flavor of a charged meson has the same sign as the meson's electric charge.
2. If the second quark has also flavor (it is not u or d) then the identity of that second quark is given by a subindex (s, c or b, and in theory t).
3. A "*" superindex is added if the meson is in the normal spin-parity series, that is, JP = 0+, 1−, 2+…
4. For mesons other than pseudoscalars (0−) and vectors (1−) the total angular momentum quantum number J is added as a subindex.
To summarize:
| quark composition | Isospin | JP = 0−, 1+, 2−... | JP = 0+, 1−, 2+... |
|---|---|---|---|
| 1/2 | † | ||
| 1/2 | |||
| 0 | |||
| 1/2 | |||
| 0 | |||
| 0 |
- † J is omitted for 0− and 1−
In some cases, particles can mix between them. For example, the neutral kaon, and its antiparticle can combine in a symmetric or antisymmetric manner, originating two new particles, the short-lived and the long-lived neutral kaons (neglecting a small CP-violating term).
See also
- Antimatter
- Atom
- Baryon
- Dark matter
- Fermion
- Hadron
- Hideki Yukawa
- Lepton
- Matter
- Neutron
- Particle physics
- Proton
- Quark
- Standard Model
- Subatomic particle
Notes
- ↑ Quarks and antiquarks that impart quantum numbers to hadrons are called "valence" quarks. In addition, any hadron may contain an indefinite number of virtual quarks, antiquarks and gluons that contribute nothing to the quantum numbers. Such virtual quarks are called "sea" quarks.
- ↑ Virtual particles are particles that cannot be observed experimentally but are thought to be involved in physical processes. See Real and Virtual Particles Retrieved September 12, 2008.
- ↑ 3.0 3.1 3.2 Hadrons: Baryons and Mesons Stanford Linear Accelerator Center. Retrieved September 11, 2008.
ReferencesISBN links support NWE through referral fees
- Cottingham, W.N., and D.A. Greenwood. 2007. An Introduction to the Standard Model of Particle Physics, 2nd ed. Cambridge, UK: Cambridge University Press. ISBN 978-0521852494.
- Griffiths, David J. 1987. Introduction to Elementary Particles. New York: Wiley. ISBN 0471603864.
- Martin, B.R. 2006. Nuclear and Particle Physics: An Introduction. Chichester: John Wiley. ISBN 978-0470025321.
- Povh, Bogdan. 1995. Particles and Nuclei: An Introduction to the Physical Concepts. Berlin: Springer-Verlag. ISBN 0387594396.
- Santra, A.B., S. Kailas, and R.S. Bhalerao (eds.). 2004. Mesons and Quarks. Workshop on 'Mesons and Quarks.' New Delhi: Narosa Pub. House.
- Veltman, Martinus. 2003. Facts and Mysteries in Elementary Particle Physics. River Edge, NJ: World Scientific. ISBN 981238149X.
External links
All links retrieved November 9, 2022.
- Mesons (A table of mesons and their properties.)
- Mesons
- The Review of Particle Physics Particle Data Group. (Authoritative information on particle properties.)
- Roos, M., and C.G. Wohl. 2004. Naming Scheme for Hadrons Particle Data Group.
- Van Beveran, Eef, et al. 2002. The light scalar mesons within quark models
- Fermilab's CDF scientists make it official: They have discovered the quick-change behavior of the Bs meson, which switches between matter and antimatter 3 trillion times a second Fermilab Press Release, September 25, 2006.
| Particles in physics | |
|---|---|
| elementary particles | Elementary fermions: Quarks: u · d · s · c · b · t • Leptons: e · μ · τ · νe · νμ · ντ Elementary bosons: Gauge bosons: γ · g · W± · Z0 • Ghosts |
| Composite particles | Hadrons: Baryons(list)/Hyperons/Nucleons: p · n · Δ · Λ · Σ · Ξ · Ω · Ξb • Mesons(list)/Quarkonia: π · K · ρ · J/ψ · Υ Other: Atomic nucleus • Atoms • Molecules • Positronium |
| Hypothetical elementary particles | Superpartners: Axino · Dilatino · Chargino · Gluino · Gravitino · Higgsino · Neutralino · Sfermion · Slepton · Squark Other: Axion · Dilaton · Goldstone boson · Graviton · Higgs boson · Tachyon · X · Y · W' · Z' |
| Hypothetical composite particles | Exotic hadrons: Exotic baryons: Pentaquark • Exotic mesons: Glueball · Tetraquark Other: Mesonic molecule |
| Quasiparticles | Davydov soliton · Exciton · Magnon · Phonon · Plasmon · Polariton · Polaron |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.