Inclined plane
The inclined plane is one of the classical simple machines. As the name suggests, it is a flat surface held at an angle to the horizontal. By moving an object up an inclined plane rather than directly from one height to another, the amount of force required is reduced, at the expense of increasing the distance the object must travel. Some examples of inclined planes are a children's slide, a loading ramp, aircraft wings, windmills, and propeller blades.
History
The inclined plane is one of the simple machines of antiquity. Their physical operations were first theorized by Archimedes in the second century B.C.E., then further explained by Hero of Alexandria in the first century C.E.
Around 2600 B.C.E., inclined planes in the form of ramps were used, at least in part, to raise the blocks of stone that make up the Great Pyramid. Between 1900 and 1400 B.C.E., inclined planes might also have been used to elevate and place large stone crosspieces at Stonehenge.
Before the advent of inclined planes, levers, pulleys, cranes, gears, and belts, heavy objects had to be hoisted, moved, and positioned by brute force.[1]
Examples of inclined planes
Examples where "inclined planes" are to be found include ramps, sloping roads, hills, windshields, funnels, children's slides, water slides, and carpenter's planes. Other examples include aircraft wings, helicopter rotors, propellers (for aircraft and boats), windmills, water wheels, turbine blades, rotary fan blades, and machine screws.
A wedge may be thought of as a portable, double inclined plane. It is used to separate two objects, or portions of objects, through the application of force. Examples of wedges include axes, spears, arrowheads, chisels, hatchets, and air hammers. Yet there is a difference between a stationary inclined plane and a wedge. While a load is moved along a stationary inclined plane, a wedge itself moves a stationary load.
Physics of the inclined plane
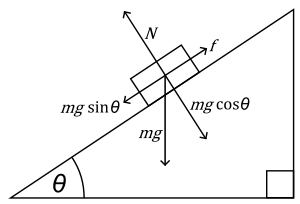
N = Normal force that is perpendicular to the plane
m = Mass of object
g = Acceleration due to gravity
θ (theta) = Angle of elevation of the plane, measured from the horizontal
f = frictional force of the inclined plane.
When an object is moved up an inclined plane rather than vertically, the amount of force needed is reduced, but the object has to be moved through a longer distance. As a result, the amount of mechanical work done in moving an object up an inclined plane is the same as the work needed to lift the object vertically.
The mechanical advantage of an inclined plane is the ratio of the length of the sloped surface to the height it spans. It may also be expressed as the cosecant of the angle between the plane and the horizontal.
The inclined plane may be understood by an elementary physics exercise. If an object is placed on an inclined plane, the forces acting on that object can be described mathematically. There are three forces acting on the body (neglecting air resistance):
- the normal force ('N') exerted by the plane onto the body,
- the force due to gravity ('mg' - acting vertically downwards), and
- the frictional force ('f') acting parallel to the plane.
The gravitational force may be visualized as having two components: A force parallel to the plane ('mgSinθ') and a force acting into the plane ('mgCosθ') which is equal and opposite to 'N'. If the force acting parallel to the plane ('mgSinθ') is greater than the frictional force 'f', then the body will slide down the inclined plane; otherwise, it will remain stationary. When the slope angle ('θ') is zero, sinθ is also zero so the body does not move.
See also
Notes
- ↑ BookRags. 2007. Inclined Plane World of Invention. Retrieved November 18, 2007.
ReferencesISBN links support NWE through referral fees
- Dahl, Michael. 1999. Inclined Planes (Simple Machines). Mankato, MN: Bridgestone Books. ISBN 1560654473
- Thompson, Gare. 2006. Science Chapters: Lever, Screw, and Inclined Plane: The Power of Simple Machines (Science Chapters). Washington DC: National Geographic Children's Books. ISBN 0792259491
- Tieck, Sarah. 2006. Inclined Planes (Simple Machines). Edina, MN: Buddy Books. ISBN 1596798181
External links
All links retrieved February 28, 2018.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.