Atomic nucleus
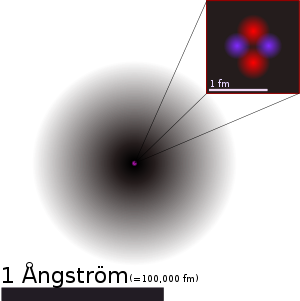
The nucleus of an atom is the very dense region at the center of the atom, consisting of particles known as protons and neutrons (collectively called nucleons). Almost all of the mass of an atom is attributable to the protons and neutrons in the nucleus, with a very small contribution from the electrons that occupy orbitals around the nucleus. The branch of physics concerned with studying and understanding the atomic nucleus, including its composition and the forces which bind it together, is called nuclear physics.
Etymology
The term nucleus is from Latin nucleus ("kernel"), derived from nux ("nut"). In 1844, Michael Faraday used the term to refer to the "central point of an atom." The modern atomic meaning was proposed by Ernest Rutherford in 1912.[1] The adoption of the term "nucleus" to atomic theory, however, was not immediate. In 1916, for example, Gilbert N. Lewis stated, in his famous article The Atom and the Molecule, that "the atom is composed of the kernel and an outer atom or shell."[2]
Nuclear makeup
As noted above, the nucleus of an atom consists of protons and neutrons. For a given chemical element, every atom has a constant number of protons in the nucleus, and this number is called the atomic number.
Each proton carries a single positive charge, and the total electrical charge of the nucleus is usually spread fairly uniformly throughout its body. However, the nuclei of hydrogen and helium atoms are exceptions, as the nuclear charge is concentrated most highly at the central point.[3] As each proton carries a unit of charge, the charge distribution is indicative of the proton distribution, and the neutron distribution is thought to be similar.[3]
The diameter of the nucleus is in the range of 1.6 femtometer (fm) (1.6 × 10−15 m) (for a proton in light hydrogen) to about 15 fm (for the heaviest atoms, such as uranium). These dimensions are much smaller than the size of the atom itself by a factor of about 23,000 (for uranium) to about 145,000 (for hydrogen).
Protons and neutrons
Protons and neutrons are classified as baryons and as composite fermions. In the atomic nucleus, protons and neutrons are bound together by the nuclear force known as the residual strong force. These baryons are further composed of fundamental particles known as quarks, which are bound by the strong interaction.
Protons and neutrons have different values of the isospin quantum number, so two protons and two neutrons can share the same space wave function. They are sometimes viewed as two different states of the same particle, the nucleon.[4][5]
In the rare case of a hypernucleus, a third baryon called a hyperon, with a different value of the strangeness quantum number, can also share the wave function. However, the latter type of nuclei are extremely unstable and are not found on Earth except in high energy physics experiments.
The neutron has a positively charged core of radius of approximate size 0.3 fm surrounded by a compensating negative charge of radius between 0.3 fm and 2 fm. The proton has an approximately exponentially decaying charge distribution with a mean square radius of about 0.8 fm.[6]
Forces
As mentioned above, protons and neutrons in a nucleus are bound together by the residual strong force. This force is a minor residuum of the strong force that binds quarks together to form protons and neutrons. This force is much weaker between neutrons and protons because it is mostly neutralized within them, in the same way that electromagnetic forces between neutral atoms (van der Waals forces) are much weaker than the electromagnetic forces that hold the atoms internally together.
The strong force is so named because it is significantly larger in magnitude than the other fundamental forces (electroweak, electromagnetic and gravitational). The strong force is highly attractive at very small distances, and this overwhelms the repulsion between protons due to the electromagnetic force, thus allowing nuclei to exist. However, because the residual strong force has a limited range, only nuclei smaller than a certain size can be completely stable. The largest known complete stable nucleus is lead-208 which contains 208 neutrons and protons. Nuclei larger than this maximal size of 208 particles generally become increasingly short-lived as the number of neutrons and protons which compose them increases beyond this number.
The residual strong force usually acts over a very short range (a few fermis, roughly one or two nucleon diameters) and causes an attraction between nucleons. However there are also halo nuclei such as lithium-11 or boron-14, in which dineutrons or other collections of nucleons orbit at distances of about ten fermis (similar to the size of lead-208). Such nuclei are always short-lived; for example, lithium-11 has a half-life of less than 8.6 milliseconds.
Nuclear models
The nuclear radius (R) is considered one of the basic features that any model must explain. It is roughly proportional to the cube root of the mass number (A) of the nucleus, particularly in nuclei containing many nucleons, as they are arranged in more spherical configurations.
The nucleus has approximately a constant density, and therefore the nuclear radius R can be approximated by the following formula:
where A = Atomic mass number (the number of protons (Z) plus the number of neutrons (N)) and = 1.25 fm = 1.25 x m.
In this equation, the constant varies by .2 fm, depending on the nucleus in question, but this is less than 20 percent change from a constant.[7]
In other words, packing protons and neutrons in the nucleus gives approximately the same total size result as packing hard spheres of a constant size (like marbles) into a tight bag.
Liquid drop models
Early models of the nucleus viewed the nucleus as a rotating liquid drop. In this model, the trade-off of long-range electromagnetic forces and relatively short-range nuclear forces, together cause behavior which resembled surface tension forces in liquid drops of different sizes. This formula is successful at explaining many important phenomena of nuclei, such as their changing amounts of binding energy as their size and composition changes, but it does not explain the special stability that is found when nuclei have special "magic numbers" of protons or neutrons.
Shell models and other quantum models
A number of models for the nucleus have also been proposed in which nucleons occupy orbitals, much like the atomic orbitals in atomic physics theory. These wave models imagine nucleons to be either sizeless point particles in potential wells, or else probability waves as in the "optical model," frictionlessly orbiting at high speed in potential wells.
In these models, the nucleons occupy orbitals in pairs, as they are fermions, but the exact nature and capacity of nuclear shells differs somewhat from those of electrons in atomic orbitals. This is primarily because the potential well in which the nucleons move (especially in larger nuclei) is quite different from the central electromagnetic potential well that binds electrons in atoms. Nevertheless, the resemblance to atomic orbital models may be seen in a small atomic nucleus like that of helium-4, in which the two protons and two neutrons separately occupy 1s orbitals analogous to the 1s orbitals for the two electrons in the helium atom, and achieve unusual stability for the same reason. This stability also underlies the fact that nuclei with five nucleons are all extremely unstable and short-lived.
For larger nuclei, the shells occupied by nucleons begin to differ significantly from electron shells. Nevertheless, present nuclear theory does predict the "magic numbers" of filled nuclear shells for both protons and neutrons. The closure of the stable shells predicts unusually stable configurations, analogous to the group of nearly-inert noble gases in chemistry. An example is the stability of the closed shell of 50 protons, which allows tin to have ten stable isotopes, more than any other element. Similarly, the distance from shell-closure explains the unusual instability of isotopes which have far from stable numbers of these particles, such as the radioactive elements 43 (technetium) and 61 (promethium), each of which is preceded and followed by 17 or more stable elements.
Consistency between models
As with the case of helium in the superfluid state, atomic nuclei are an example of a state in which both types of rules apply: (1) "ordinary" particle physical rules for volume, and (2) non-intuitive quantum mechanical rules for a wave-like nature. In superfluid helium, the helium atoms have volume, and essentially "touch" each other, yet at the same time exhibit strange bulk properties, consistent with a Bose-Einstein condensation. The latter reveals that they also have a wave-like nature and do not exhibit standard fluid properties, such as friction.
For nuclei made of hadrons which are fermions, the same type of condensation does not occur. Nevertheless, many nuclear properties can be explained similarly by a combination of properties of particles with volume, in addition to the frictionless motion characteristic of the wave-like behavior of objects trapped in Schroedinger quantum orbitals.
See also
- Atom
- Atomic mass
- Atomic number
- Fermion
- Isotope
- Neutron
- Nuclear fusion
- Nuclear fission
- Nuclear physics
- Particle physics
- Proton
- Radioactivity
Notes
- ↑ Nucleus Online Etymology Dictionary. Retrieved November 10, 2008.
- ↑ Gilbert N. Lewis (1916), The Atom and the Molecule J. Am. Chem. Soc. 38:762-786. Retrieved November 22, 2008.
- ↑ 3.0 3.1 Jean-Louis Basdevant, James Rich, and Michel Spiro, Fundamentals in Nuclear Physics (New York, NY: Springer, 2005, ISBN 0387016724). Fig. 1.1, page 13 Retrieved November 10, 2008.
- ↑ A.G. Sitenko and Viktor Konstantinovich Tartakovskiĭ, Theory of Nucleus: Nuclear Structure and Nuclear Interaction (Dordrecht, NL; Boston, MA: Kluwer Academic, 1997, ISBN 0792344235). page 3 Retrieved November 10, 2008.
- ↑ Mark Allen Srednicki, Quantum Field Theory (Cambridge, UK: Cambridge University Press, 2007, ISBN 9780521864497), 522-523.
- ↑ Rich Basdevant and Spiro (2005), Fig. 3.23. page 155 Retrieved November 10, 2008.
- ↑ Kenneth S. Krane and David Halliday, Introductory Nuclear Physics (New York, NY: Wiley, 1987, ISBN 9780471805533).
ReferencesISBN links support NWE through referral fees
- Basdevant, Jean-Louis, James Rich, and Michel Spiro. 2005. Fundamentals in Nuclear Physics. New York, NY: Springer. ISBN 0387016724
- Krane, Kenneth S., and David Halliday. 1987. Introductory Nuclear Physics. New York, NY: Wiley. ISBN 9780471805533
- Sitenko, A.G., and Viktor Konstantinovich Tartakovskiĭ. 1997. Theory of Nucleus: Nuclear Structure and Nuclear Interaction. Dordrecht, NL; Boston, MA: Kluwer Academic. ISBN 0792344235
- Srednicki, Mark Allen. 2007. Quantum Field Theory. Cambridge, UK: Cambridge University Press. ISBN 9780521864497
| Particles in physics | |
|---|---|
| elementary particles | Elementary fermions: Quarks: u · d · s · c · b · t • Leptons: e · μ · τ · νe · νμ · ντ Elementary bosons: Gauge bosons: γ · g · W± · Z0 • Ghosts |
| Composite particles | Hadrons: Baryons(list)/Hyperons/Nucleons: p · n · Δ · Λ · Σ · Ξ · Ω · Ξb • Mesons(list)/Quarkonia: π · K · ρ · J/ψ · Υ Other: Atomic nucleus • Atoms • Molecules • Positronium |
| Hypothetical elementary particles | Superpartners: Axino · Dilatino · Chargino · Gluino · Gravitino · Higgsino · Neutralino · Sfermion · Slepton · Squark Other: Axion · Dilaton · Goldstone boson · Graviton · Higgs boson · Tachyon · X · Y · W' · Z' |
| Hypothetical composite particles | Exotic hadrons: Exotic baryons: Pentaquark • Exotic mesons: Glueball · Tetraquark Other: Mesonic molecule |
| Quasiparticles | Davydov soliton · Exciton · Magnon · Phonon · Plasmon · Polariton · Polaron |
| Nuclear technology | |
|---|---|
| Nuclear engineering | Nuclear physics | Nuclear fission | Nuclear fusion | Radiation | Ionizing radiation | Atomic nucleus | Nuclear reactor | Nuclear safety |
| Nuclear material | Nuclear fuel | Fertile material | Thorium | Uranium | Enriched uranium | Depleted uranium | Plutonium |
| Nuclear power | Nuclear power plant | Radioactive waste | Fusion power | Future energy development | Inertial fusion power plant | Pressurized water reactor | Boiling water reactor | Generation IV reactor | Fast breeder reactor | Fast neutron reactor | Magnox reactor | Advanced gas-cooled reactor | Gas-cooled fast reactor | Molten salt reactor | Liquid-metal-cooled reactor | Lead-cooled fast reactor | Sodium-cooled fast reactor | Supercritical water reactor | Very high temperature reactor | Pebble bed reactor | Integral Fast Reactor | Nuclear propulsion | Nuclear thermal rocket | Radioisotope thermoelectric generator |
| Nuclear medicine | PET | Radiation therapy | Tomotherapy | Proton therapy | Brachytherapy |
| Nuclear weapons | History of nuclear weapons | Nuclear warfare | Nuclear arms race | Nuclear weapon design | Effects of nuclear explosions | Nuclear testing | Nuclear delivery | Nuclear proliferation | List of states with nuclear weapons | List of nuclear tests |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.


