Aerodynamics

Aerodynamics is a branch of fluid dynamics concerned with studying the principles of the flow of gases and the forces generated on a solid body within the flow. To solve a problem in aerodynamics, the researcher needs to take into account various properties of the flow, such as velocity, pressure, density, and temperature, as functions of space and time. By understanding the flow pattern, it becomes possible to calculate or estimate the forces and moments acting on solid bodies within the flow.
Aerodynamics forms the scientific basis for heavier-than-air flight. In addition, it plays an important role in the design of automobiles, large buildings, bridges, ventilation passages, and hard drive heads. Town planners need to consider aerodynamics to reduce pollution and increase comfort in outdoor spaces, and environmental scientists study aerodynamics to understand air circulation and how flight mechanics affect ecosystems.
History
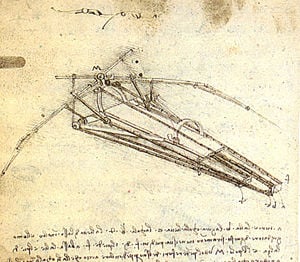
Images and stories of flight have appeared throughout recorded history. One of the most notable of these is the story of Icarus and Daedalus.[1] Although observations of some aerodynamic effects, such as wind resistance (or drag) were recorded by the likes of Aristotle and Galileo Galilei, very little effort was made to develop governing laws for understanding the nature of flight prior to the seventeenth century.
Sir Isaac Newton was the first person to develop a theory of air resistance in 1726,[2] arguably making him the world's first aerodynamicist. As part of that theory, Newton believed that drag was due to the dimensions of a body, the density of the fluid, and the velocity raised to the second power. These ideas all turned out to be correct for low-flow speeds. Newton also developed a law for the drag force on a flat plate inclined toward the direction of the fluid flow. Using F for the drag force, ρ for the density, S for the area of the flat plate, V for the flow velocity, and θ for the inclination angle, his law was expressed by the following equation:
Unfortunately, this equation is entirely incorrect for the calculation of drag (unless the flow speed is hypersonic). Drag on a flat plate is closer to being linear with the angle of inclination as opposed to acting quadratically. This formula can lead one to believe that flight is more difficult than it actually is, and it may have contributed to a delay in manned flight.[3]
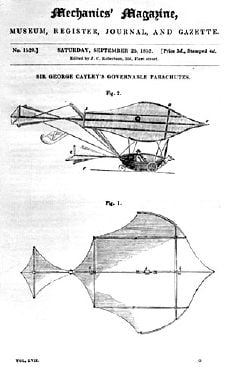
Sir George Cayley is credited as the first person to separate the forces of lift and drag which are in effect on any flight vehicle. Cayley believed that the drag on a flying machine must be counteracted by a means of propulsion in order for level flight to occur. Cayley also looked to nature for aerodynamic shapes with low drag. One of the shapes he investigated were the cross-sections of trout. The bodies of fish are shaped to produce very low resistance as they travel through water. As such, their cross-sections are sometimes very close to that of modern low-drag airfoils.
These empirical findings led to a variety of air resistance experiments on various shapes throughout the eighteenth and nineteenth centuries. Drag theories were developed by Jean le Rond d'Alembert,[4] Gustav Kirchhoff,[5] and Lord Rayleigh.[6] Equations for fluid flow with friction were developed by Claude-Louis Navier[7] and George Gabriel Stokes.[8] To simulate fluid flow, many experiments involved immersing objects in streams of water or simply dropping them off the top of a tall building. Towards the end of this time period, Gustave Eiffel used his Eiffel Tower to assist in the drop testing of flat plates.
A more precise way to measure resistance is to place an object within an artificial, uniform stream of air where the velocity is known. The first person to experiment in this fashion was Francis Herbert Wenham, who in doing so constructed the first wind tunnel in 1871. Wenham was also a member of the first professional organization dedicated to aeronautics, the Royal Aeronautical Society of Great Britain. Objects placed in wind tunnel models are almost always smaller than in practice, so a method was needed to relate small scale models to their real-life counterparts. This was achieved with the invention of the dimensionless Reynolds number by Osbourne Reynolds.[9] Reynolds also experimented with laminar to turbulent flow transition in 1883.
By the late nineteenth century, two problems were identified before heavier-than-air flight could be realized. The first was the creation of low-drag, high-lift aerodynamic wings. The second problem was how to determine the power needed for sustained flight. During this time, the groundwork was laid down for modern day fluid dynamics and aerodynamics, with other less scientifically inclined enthusiasts testing various flying machines with little success.

In 1889, Charles Renard, a French aeronautical engineer, became the first person to reasonably predict the power needed for sustained flight.[10] Renard and German physicist Hermann von Helmholtz explored the wing loading of birds, eventually concluding that humans could not fly under their own power by attaching wings onto their arms. Otto Lilienthal, following the work of Sir George Cayley, was the first person to become highly successful with glider flights. Lilienthal believed that thin, curved airfoils would produce high lift and low drag.
Octave Chanute provided a great service to those interested in aerodynamics and flying machines by publishing a book outlining all of the research conducted around the world up to 1893.[11] With the information contained in that book and the personal assistance of Chanute himself, the Wright brothers had just enough knowledge of aerodynamics to fly the first manned aircraft on December 17, 1903, just in time to beat the efforts of Samuel Pierpont Langley. The Wright brothers' flight confirmed or disproved a number of aerodynamics theories. Newton's drag force theory was finally proved incorrect. The first flight led to a more organized effort between aviators and scientists, leading the way to modern aerodynamics.
During the time of the first flights, Frederick W. Lanchester,[12] Martin Wilhelm Kutta, and Nikolai Zhukovsky independently created theories that connected circulation of a fluid flow to lift. Kutta and Zhukovsky went on to develop a two-dimensional wing theory. Expanding upon the work of Lanchester, Ludwig Prandtl is credited with developing the mathematics[13] behind thin-airfoil and lifting-line theories as well as work with boundary layers. Prandtl, a professor at Gottingen University, instructed many students who would play important roles in the development of aerodynamics like Theodore von Kármán and Max Munk.
As aircraft began to travel faster, aerodynamicists realized that the density of air began to change as it came into contact with an object, leading to a division of fluid flow into the incompressible and compressible regimes. In compressible aerodynamics, density and pressure both change, which is the basis for calculating the speed of sound. Newton was the first to develop a mathematical model for calculating the speed of sound, but it was not correct until Pierre-Simon Laplace accounted for the molecular behavior of gases and introduced the heat capacity ratio. The ratio of the flow speed to the speed of sound was named the Mach number after Ernst Mach, who was one of the first to investigate the properties of supersonic flow which included Schlieren photography techniques to visualize the changes in density. William John Macquorn Rankine and Pierre Henri Hugoniot independently developed the theory for flow properties before and after a shock wave. Jakob Ackeret led the initial work on calculating the lift and drag on a supersonic airfoil.[14] Theodore von Kármán and Hugh Latimer Dryden introduced the term transonic to describe flow speeds around Mach 1 where drag increases rapidly. Because of the increase in drag approaching Mach 1, aerodynamicists and aviators disagreed on whether manned supersonic flight was achievable.
On September 30, 1935 an exclusive conference was held in Rome with the topic of high velocity flight and the possibility of breaking the sound barrier.[15] Participants included von Kármán, Prandtl, Ackeret, Eastman Jacobs, Adolf Busemann, Geoffrey Ingram Taylor, Gaetano Arturo Crocco, and Enrico Pistolesi. The new research presented was impressive. Ackeret presented a design for a supersonic wind tunnel. Busemann gave perhaps the best presentation on the need for aircraft with swept wings for high speed flight. Eastman Jacobs, working for NACA, presented his optimized airfoils for high subsonic speeds which led to some of the high performance American aircraft during World War II. Supersonic propulsion was also discussed. The sound barrier was broken using the Bell X-1 aircraft twelve years later, thanks in part to those individuals.
By the time the sound barrier was broken, much of the subsonic and low supersonic aerodynamics knowledge had matured. The Cold War fueled an ever evolving line of high performance aircraft. Computational fluid dynamics was started as an effort to solve for flow properties around complex objects and has rapidly grown to the point where entire aircraft can be designed using a computer.
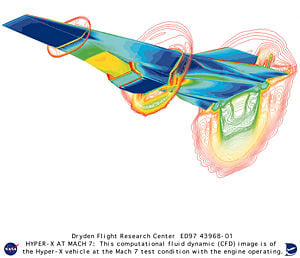
With some exceptions, the knowledge of hypersonic aerodynamics has matured between the 1960s and the present decade. Therefore, the goals of an aerodynamicist have shifted from understanding the behavior of fluid flow to understanding how to engineer a vehicle to interact appropriately with the fluid flow. For example, while the behavior of hypersonic flow is understood, building a scramjet aircraft to fly at hypersonic speeds has met with very limited success. Along with building a successful scramjet aircraft, the desire to improve the aerodynamic efficiency of current aircraft and propulsion systems will continue to fuel new research in aerodynamics.
Aerodynamic problems: classification
Aerodynamic problems can be classified in a number of ways. The flow environment defines the first classification criterion. External aerodynamics is the study of flow around solid objects of various shapes. Examples of external aerodynamics include evaluation of the lift and drag on an airplane, the shock waves that form in front of a rocket's nose, or the flow of air over a hard drive head. Internal aerodynamics is the study of flow through passages in solid objects. Internal aerodynamics encompasses, for instance, the study of airflow through a jet engine or through an air conditioning pipe.
The ratio of the fluid's characteristic flow speed to the speed of sound constitutes a second type of classification of aerodynamic problems. A problem is called subsonic if all the speeds in the problem are less than the speed of sound; transonic if flow speeds both below and above the speed of sound are present (normally when the characteristic speed is approximately the speed of sound); supersonic when the characteristic flow speed is greater than the speed of sound; and hypersonic when the flow speed is much greater than the speed of sound. Aerodynamicists disagree over the precise definition of hypersonic flow; minimum Mach numbers for hypersonic flow range from 3 to 12. Most aerodynamicists use Mach numbers between 5 and 8.
The influence of viscosity in the flow dictates a third type of classification. Some problems involve negligible viscous effects on the solution, in which case viscosity may be considered nonexistent. Approximations to these problems are called inviscid flows. Flows for which viscosity cannot be neglected are called viscous flows.
Continuity assumption
Gases are composed of molecules that collide with one another and solid objects. If density and velocity are taken to be well-defined at infinitely small points, and they are assumed to vary continuously from one point to another, the discrete molecular nature of a gas is ignored.
The continuity assumption becomes less valid as a gas becomes increasingly rarefied. In these cases, statistical mechanics is a more valid method of solving the problem than aerodynamics.
Conservation laws
Aerodynamic problems are solved using the conservation laws, or equations derived from the conservation laws. In aerodynamics, three conservation laws are used:
- Conservation of mass: Matter is not created or destroyed. If a certain mass of fluid enters a volume, it must either exit the volume or increase the mass inside the volume.
- Conservation of momentum: This is also called Newton's second law of motion.
- Conservation of energy: Although energy can be converted from one form to another, the total energy in a given system remains constant.
Incompressible aerodynamics
An incompressible flow is characterized by a constant density despite flowing over surfaces or inside ducts. A flow can be considered incompressible as long as its speed is low. For higher speeds, the flow will begin to compress as it comes into contact with surfaces. The Mach number is used to distinguish between incompressible and compressible flows.
Subsonic flow
Subsonic (or low-speed) aerodynamics is the study of inviscid, incompressible and irrotational aerodynamics where the differential equations used are a simplified version of the governing equations of fluid dynamics.[16] It is a special case of Subsonic aerodynamics.
In solving a subsonic problem, one decision to be made by the aerodynamicist is whether to incorporate the effects of compressibility. Compressibility is a description of the amount of change of density in the problem. When the effects of compressibility on the solution are small, the aerodynamicist may choose to assume that density is constant. The problem is then an incompressible low-speed aerodynamics problem. When the density is allowed to vary, the problem is called a compressible problem. In air, compressibility effects are usually ignored when the Mach number in the flow does not exceed 0.3 (about 335 feet per second or 228 miles per hour or 102 meters per second at 60oF). Above 0.3, the problem should be solved using compressible aerodynamics.
Compressible aerodynamics
According to the theory of aerodynamics, a flow is considered to be compressible if its change in density with respect to pressure is non-zero along a streamline. In short, this means that, unlike incompressible flow, changes in density must be considered. In general, this is the case where the Mach number in part or all of the flow exceeds 0.3. The Mach .3 value is rather arbitrary, but it is used because gas flows with a Mach number below that value demonstrate changes in density with respect to the change in pressure of less than 5%. Furthermore, that maximum 5% density change occurs at the stagnation point of an object immersed in the gas flow and the density changes around the rest of the object will be significantly lower. Transonic, supersonic, and hypersonic flows are all compressible.
Transonic flow
The term Transonic refers to a range of velocities just below and above the local speed of sound (generally taken as Mach 0.8–1.2). It is defined as the range of speeds between the critical Mach number, when some parts of the airflow over an aircraft become supersonic, and a higher speed, typically near Mach 1.2, when all of the airflow is supersonic. Between these speeds some of the airflow is supersonic, and some is not.
Supersonic flow
Supersonic aerodynamic problems are those involving flow speeds greater than the speed of sound. Calculating the lift on the Concorde during cruise can be an example of a supersonic aerodynamic problem.
Supersonic flow behaves very differently from subsonic flow. Fluids react to differences in pressure; pressure changes are how a fluid is "told" to respond to its environment. Therefore, since sound is in fact an infinitesimal pressure difference propagating through a fluid, the speed of sound in that fluid can be considered the fastest speed that "information" can travel in the flow. This difference most obviously manifests itself in the case of a fluid striking an object. In front of that object, the fluid builds up a stagnation pressure as impact with the object brings the moving fluid to rest. In fluid traveling at subsonic speed, this pressure disturbance can propagate upstream, changing the flow pattern ahead of the object and giving the impression that the fluid "knows" the object is there and is avoiding it. However, in a supersonic flow, the pressure disturbance cannot propagate upstream. Thus, when the fluid finally does strike the object, it is forced to change its properties — temperature, density, pressure, and Mach number — in an extremely violent and irreversible fashion called a shock wave. The presence of shock waves, along with the compressibility effects of high-velocity (see Reynolds number) fluids, is the central difference between supersonic and subsonic aerodynamics problems.
Hypersonic flow
In aerodynamics, hypersonic speeds are speeds that are highly supersonic. In the 1970s, the term generally came to refer to speeds of Mach 5 (5 times the speed of sound) and above. The hypersonic regime is a subset of the supersonic regime. Hypersonic flow is characterized by high temperature flow behind a shock wave, viscous interaction, and chemical dissociation of gas.
Associated terminology
The incompressible and compressible flow regimes produce many associated phenomena, such as boundary layers and turbulence.
Boundary layers
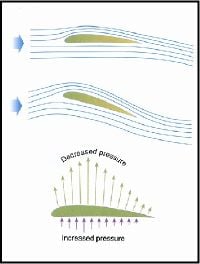
The concept of a boundary layer is important in many aerodynamic problems. The viscosity and fluid friction in the air is approximated as being significant only in this thin layer. This principle makes aerodynamics much more tractable mathematically.
Turbulence
In aerodynamics, turbulence is characterized by chaotic, stochastic property changes in the flow. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. Flow that is not turbulent is called laminar flow.
Applications of aerodynamics in diverse fields
Aerodynamics is important in a number of applications other than aerospace engineering. For instance, it is a significant factor in any type of vehicle design, including automobiles. It is important in the prediction of forces and moments in sailing. It is used in the design of small components such as hard drive heads.
Structural engineers use aerodynamics, particularly aeroelasticity, to calculate wind loads in the design of large buildings and bridges. Urban aerodynamics helps town planners and designers improve comfort in outdoor spaces, create urban micro climates, and reduce the effects of urban pollution. The field of environmental aerodynamics studies the ways atmospheric circulation and flight mechanics affect ecosystems. The aerodynamics of internal passages is important in heating/ventilation, gas piping, and in automotive engines, where detailed flow patterns strongly affect the performance of the engine.
See also
Notes
- ↑ Ovid, Horace Gregory (trans.), The Metamorphoses (Signet Classics, 2001, ISBN 978-0451527936).
- ↑ Isaac Newton, Philosophiae Naturalis Principia Mathematica, Book II (English) (CreateSpace, 2018, ISBN 978-1726337984).
- ↑ Theodore von Karman, Aerodynamics: Selected Topics in the Light of Their Historical Development (Dover Publications, 2004, ISBN 978-0486434858).
- ↑ Jean le Rond d'Alembert, Essai d'une nouvelle theorie de la resistance des fluides (1752).
- ↑ Gustav Kirchhoff, "Zur Theorie freier Flussigkeitsstrahlen" Journal fur die reine und angewandte Mathematik (70) (1869):289-298.
- ↑ John Strutt, Lord Rayleigh, "On the Resistance of Fluids" Philosophical Magazine (5)2 (1876):430-441.
- ↑ C.L.M.H. Navier, Memoire sur les lois du mouvement des fluides (Memoires de l'Academie des Sciences (6) (1823): 389-416.
- ↑ G. Stokes, G. On the Theories of the Internal Friction of Fluids in Motion (Transaction of the Cambridge Philosophical Society (8) (1845:287-305.
- ↑ O. Reynolds, An Experimental Investigation of the Circumstances which Determine whether the Motion of Water Shall Be Direct or Sinuous and of the Law of Resistance in Parallel Channels (Philosophical Transactions of the Royal Society of London A-174, (1883): 935-982.
- ↑ C. Renard, Nouvelles experiences sur la resistance de l'air L'Aeronaute (22) (1889): 73-81.
- ↑ Octave Chanute, Progress in Flying Machines (Dover Publications, 1997, ISBN 0486299813).
- ↑ F.W. Lanchester, Aerodynamics (University of Michigan Library, 1908).
- ↑ Ludwig Prandtl, Tragflugeltheorie (Gottinger Nachrichten, mathematischphysikalische Klasse, (1919): 451-477.
- ↑ Jakob Ackeret, Luftkrafte auf Flugel, die mit der grosserer als Schallgeschwindigkeit bewegt werden (Zeitschrift fur Flugtechnik und Motorluftschiffahrt (16) (1925): 72-74.
- ↑ John David Anderson, Fundamentals of Aerodynamics (McGraw-Hill, 2007, ISBN 0071254080).
- ↑ Joseph Katz, Low-speed aerodynamics: from wing theory to panel methods (McGraw-Hill, 1991).
ReferencesISBN links support NWE through referral fees
- Abbott, Ira H., and A.E. von Doenhoff. Theory of Wing Sections: Including a Summary of Airfoil Data. Mineola, NY: Dover Publications, 1959. ISBN 0486605868.
- Anderson, John David. A History of Aerodynamics, and Its Impact on Flying Machines. Cambridge Aerospace Series, 8. Cambridge: Cambridge University Press, 1997. ISBN 0521454352.
- Anderson, John David. Fundamentals of Aerodynamics. 4th ed. McGraw-Hill Series in Aeronautical and Aerospace Engineering. Boston: McGraw-Hill Higher Education, 2007. ISBN 978-0071254083.
- Anderson, John David. Introduction to Flight. 6th ed. Dubuque, IA: McGraw-Hill, 2007. ISBN 978-0073529394.
- Ashley, Holt, and Marten Landahl. Aerodynamics of Wings and Bodies. 2nd ed. Mineola, NY: Dover Publications, 1985. ISBN 0486648990.
- Barnard, R. H. Road Vehicle Aerodynamic Design. 2nd ed. St Albans: MechAero, 2001. ISBN 0954073401.
- Chanute, Octave. Progress in Flying Machines. Mineola, NY: Dover Publications, 1997. ISBN 0486299813.
- Craig, Gale M. Introduction to Aerodynamics. Anderson, IN: Regenerative Press, 2002. ISBN 0964680637.
- Katz, Joseph. Race Car Aerodynamics: Designing for Speed. Cambridge, MA: R. Bentley, 1995. ISBN 0837601428.
- Katz, Joseph. Low-Speed Aerodynamics. Cambridge University Press, 2001. ISBN 978-0521665520
- Leishman, J. Gordon.Principles of Helicopter Aerodynamics. 2nd ed. Cambridge Aerospace Series, 18. Cambridge: Cambridge University Press, 2006. ISBN 0521858607.
- Nielson, Jack N. Missile Aerodynamics. Mountain View, CA: Nielsen Engineering & Research, 1988. ISBN 0962062901.
- Seddon, J., and Simon Newman. Basic Helicopter Aerodynamics: An Account of First Principles in the Fluid Mechanics and Flight Dynamics of the Single Rotor Helicopter. Reston, VA: American Institute of Aeronautics and Astronautics, 2001. ISBN 1563475103.
- Simons, Martin. Model Aircraft Aerodynamics. 4th ed. Swanley: Nexus Special Interests, 1999. ISBN 1854861905.
- Smith, Hubert. The Illustrated Guide to Aerodynamics. 2nd ed. Blue Ridge Summit, PA: Tab Books, 1992. ISBN 0830639012.
- Tennekes, H. The Simple Science of Flight: From Insects to Jumbo Jets. Cambridge, MA: MIT Press, 1997. ISBN 0262700654.
- Von Kármán, Theodore. Aerodynamics: Selected Topics in the Light of Their Historical Development. Mineola, NY: Dover Publications, 2004. ISBN 0486434850.
External links
All links retrieved June 15, 2023.
- What Is Aerodynamics? - NASA
- Aerodynamic Related Projects - AeroDyn Design
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.